Hexnet - Global Hexagonal Awareness Resource Center

treenshop.com article Nice article on the regular octahedron by woodturner

Creative Learning - Hexagonal Closed Packed Structure 3D Animation

youtube Creative Learning - Hexagonal Closed Packed Structure 3D Animation - abab close packing - hexagonal close packing

Oxford Academic - Understanding close packing

youtube Oxford Academic - Understanding close packing

abca or cubic-close packing - 3rd layer over gaps from first 2
abab or hexagonal-close packing - 3rd laver over 1st layer spheres

wikipedia.org Tetrahedral-octahedral honeycomb

wikipedia.org svg Exploded view of 6 oct and 4 tet around center point

wikimedia.org png larger tesselation with oct and tet

Below is my solution to these problems. These blocks can be made with ordinary two part molds. They store in a small fraction of the space occupied by the assembled bricks and they require only a fraction of the materials to manufacture.

tet delta block

local - tet delta block

oct delta block

local - oct delta block

geom.uiuc.edu article The Octahedron and the Truncated Octahedron

processing.org/discourse Here is a gift of the five platonic solid’s cartesian coordinates

math.brown.edu/~banchoff/Beyond3d Coordinates for Regular Polyhedra

mathworld.wolfram.com article Hexagonal Close Packing

hexnet.org article Close-packing of spheres

quadibloc.com/math/pakint Sphere Packing

But there is a packing which fills space that involves alternating tetrahedrons and octahedrons.

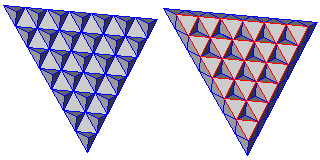
First, on a plane divided in a tesselation of triangles, we place a tetrahedron on every second triangle, in a fashion similar to the way a checkerboard is colored.

Then the other triangles have a space above each of them into which an octahedron can fit neatly.

And once these spaces are filled, there are again spaces left which are perfect for another layer of tetrahedra, forming a flat slab.

If this is continued by placing tetrahedra on top of the octahedra to start the new layer, the result will be as symmetrical as possible, and the vertices of the polyhedra will be distributed in the same manner as spheres in a face-centered cubic packing.

wow.com/wiki

Close-packing of equal spheres wow.com wiki

Miller indices

Tetrahedral-octahedral honeycomb wow.com wiki

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2.

John Horton Conway calls this honeycomb a tetroctahedrille, and its dual dodecahedrille.

        The Symmetries of Things 1st Edition
        by John H. Conway (Author), Heidi Burgiel (Author), Chaim Goodman-Strauss (Author) 
        
        Hardcover: 448 pages
        Publisher: A K Peters/CRC Press; 1 edition (April 18, 2008)
        Language: English
        ISBN-10: 1568812205
        ISBN-13: 978-1568812205

Octet Space